|
[VIEWED 5733
TIMES]
|
SAVE! for ease of future access.
|
|
|
|
spoiled

Please log in to subscribe to spoiled's postings.
Posted on 04-17-08 7:09
PM
Reply
[Subscribe]
|
Login in to Rate this Post:
0  ?
? 
|
| |
how do you prove the following identity?
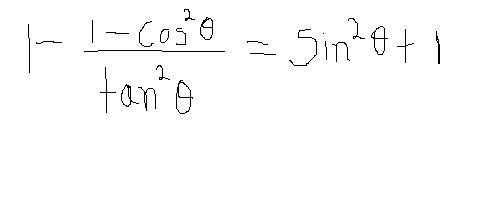
|
| |
|
|
|
|
parbatya

Please log in to subscribe to parbatya's postings.
Posted on 04-17-08 7:34
PM
Reply
[Subscribe]
|
Login in to Rate this Post:
0  ?
? 
|
| |
1. Given, 1- (1- cos2T) = sin2T +1
tan2t
1- (sin 2 T) = sin2T + 1
sin2T/cos2T
1-cos 2T = 1+ sin2T
-Cos2T = sin2T (this is not identical)
2. So square both sides : Cos4T = Sin4T
3 . Cos4T - Sin4T =0
4. (cos2T-sin2T) (cos22T+sin2T)=0
5. That gives you value of Theta as 45 degree. Am I right?
Where T=Theta.
Last edited: 17-Apr-08 08:16 PM
|
| |
|
|
parbatya

Please log in to subscribe to parbatya's postings.
Posted on 04-17-08 7:36
PM
Reply
[Subscribe]
|
Login in to Rate this Post:
0  ?
? 
|
| |
Do yo want to solve or prove????
|
| |
|
|
Lati_ko_Poi

Please log in to subscribe to Lati_ko_Poi's postings.
Posted on 04-17-08 7:38
PM
Reply
[Subscribe]
|
Login in to Rate this Post:
0  ?
? 
|
| |
I think the identity is wrong. it should be like this
(1-(1-cos2 Theta)/tan2Theta)=sin2Theta
|
| |
|
|
Lati_ko_Poi

Please log in to subscribe to Lati_ko_Poi's postings.
Posted on 04-17-08 7:52
PM
Reply
[Subscribe]
|
Login in to Rate this Post:
0  ?
? 
|
| |
If u r trying to find the value of theta, no theta satisfies the above eqn. (except some complex angle..not sure if it does).
Parbatya is wrong, put 45 back to the equation, u will be ended up with 0.5=1.5
|
| |
|
|
parbatya

Please log in to subscribe to parbatya's postings.
Posted on 04-17-08 7:56
PM
Reply
[Subscribe]
|
Login in to Rate this Post:
0  ?
? 
|
| |
Actually this is not 'identity'. They can not be solved in straight way but they have solution as I found there.
BTW I am not mathematician.
Last edited: 17-Apr-08 08:02 PM
|
| |
|
|
Lati_ko_Poi

Please log in to subscribe to Lati_ko_Poi's postings.
Posted on 04-17-08 7:57
PM
Reply
[Subscribe]
|
Login in to Rate this Post:
0  ?
? 
|
| |
Identity means despite the value of theta, the expression is correct
|
| |
|
|
jptsamachar

Please log in to subscribe to jptsamachar's postings.
Posted on 04-17-08 8:00
PM
Reply
[Subscribe]
|
Login in to Rate this Post:
0  ?
? 
|
| |
laaaaaaaaaaaaamo jasto..namilney identity raakhney ko ho yo?????????
|
| |
|
|
भउते

Please log in to subscribe to भउते's postings.
Posted on 04-17-08 8:05
PM
Reply
[Subscribe]
|
Login in to Rate this Post:
0  ?
? 
|
| |
LHS = 1- (1- cos2T)
tan2t
= 1- (sin 2 T) ------->>> 1-cos2T = sin2T & tan 2T = sin2T/cos2T
sin2T/cos2T
= 1-cos 2T
= sin 2 T------->>> 1-cos2T = sin2T
Therefore, RHS suppose to be----->> sin 2 T !! ????? 
Did I get it right !  WOW ! I better participate on the TV show " Are You Smarter Than a 5th Grader?". LOL ! :D :D :p WOW ! I better participate on the TV show " Are You Smarter Than a 5th Grader?". LOL ! :D :D :p
Last edited: 17-Apr-08 08:11 PM
|
| |
|
|
भउते

Please log in to subscribe to भउते's postings.
Posted on 04-17-08 8:27
PM
Reply
[Subscribe]
|
Login in to Rate this Post:
0  ?
? 
|
| |
मिलेन मिलेन पर्बतेदा'। त्यो जहाँ पायो त्यैँ दुइतिरै स्क्वाएर घुसाउन मिल्ने भा' भे' त १ बराबर २ देखाउन नि सकिन्छ। 
|
| |
|
|
GP

Please log in to subscribe to GP's postings.
Posted on 04-17-08 10:35
PM
Reply
[Subscribe]
|
Login in to Rate this Post:
0  ?
? 
|
| |
Here is simple solution: since theta is angle, I am not writing it at the very end. You may assume it.
1 = sin^2 + cost^2,
1/tan^2 = cos^2 / sin^2
1- cos^2 = sin^2
Use these expressions:
sin^2 + cos^2 + (1-cos^2)/tan^2 = 1 + sin^2
Cancel out common parts:
cos^2 - sin^2 * cos^2 / sin^2 = 1
cos^2 - cos^2 = 1
-cos^2 A = sin^2 A
Since there is -ve sign , and SinA and cosA are both squared term, it does not have real solution. It is April Fool problem.
|
| |
|
|
sabaiko satru

Please log in to subscribe to sabaiko satru's postings.
Posted on 04-17-08 10:50
PM
Reply
[Subscribe]
|
Login in to Rate this Post:
0  ?
? 
|
| |
Last edited: 18-Apr-08 11:29 AM
|
| |
|
|
sabaiko satru

Please log in to subscribe to sabaiko satru's postings.
Posted on 04-17-08 10:52
PM
Reply
[Subscribe]
|
Login in to Rate this Post:
0  ?
? 
|
| |
or u can bring that sin^2 on LHS and solve to prove LHS=RHS
|
| |
|
|
भउते

Please log in to subscribe to भउते's postings.
Posted on 04-17-08 11:01
PM
Reply
[Subscribe]
|
Login in to Rate this Post:
0  ?
? 
|
| |
1- 1- (sin 2 T) = 1-cos2 T कसरी हुन्छ? 
sin2T/cos2T
1- 1- (sin 2 T)
sin2T/cos2T
= 1-1-cos2T
= cos2T भएन र भन्या?
अनि सुरु देखि नै त्यो 1-1 किन बोकेर हिडि राखेको? त्यो त त्यसै 0 हुनुपर्ने। 
|
| |
